(実験)研究者のための電子状態計算法入門 [上へ][Top]
平成8年8月30日開始(2/27、2020、更新)
物理上の間違い、文法の間違い、誤字、脱字等
を見つけた場合、御指摘下されば幸いです。尚、この文書の再配布(ごく内輪的なものは可)、転載等はいまのところ御
遠慮ください。
詳しくは、著作権ページ参照。
- 目次
- はじめに
- 本論
- バンド理論とは
- 何かよくわからないバンド構造
- バンド計算(第一原理電子状態計算のみ)の種類
- all-electron法
- 擬ポテンシャル法
- カー・パリネロ法
- バンド計算はどこまで正しいか(信用できるか)
- バンド計算の限界
- あなたにもバンド計算はできるか?
- 正しい、バンド屋さんとの接し方
このページがバンド計算メニューでの、一番最初のドキュメント(テキスト、
文章)ページです。所内(旧無機材研←当時)でいろいろ意見を伺っていると、
このウェブ(WWW)ページの内容が難しいという指摘がありました。
(雑誌「表面科学」特集:第一原理計算)
上記表題による特集記事が、第28巻、第3号(2007年3月)に掲載さ
れました。筆者も、”(第一原理)バンド計算と実験との距離”という題目で
記事(同特集号、129〜134頁)を書きました。本ページの主旨とも良く
合致した内容なので、ここで紹介しておきます。
尚、同特集の他の記事も、第一原理計算に関して大変有用で勉強
になります。詳細に関しては、日本表面科学会(SSSJ)のページをご参照下さい。
電子状態計算という分野は、誰もが周知の通り理論物理(計算物理)の分野
に属し、難解な量子力学等の知識を必要(必須)とします。加えて欧米と比較
して日本での電子状態研究はあまり盛んではありません。
従って、多くの実験研究者はこの手の理論計算の詳しい内容や実体を知らな
いと思います。(実を言えば、当の本人も良く分かっていない^^;)
そこで、堅苦しい形式や難しい理屈なしに、電子状態計算に関する入門的な
話をここでしてみたいと思います。
最近は比較的優良なバンド計算のコードが、有償、無償様々な条件、ライセ
ンスで複数のところで配布(または販売)されています(参照→用語集[実践編])。まや有用な書籍、テキスト(マニュアル、ドキュメント)、
ウェブサイトなども(英語など外国語による
ものも含めて)増えてきています。
電子状態計算という言い方
他にもいろいろな呼び方があります。電子構造計算、バンド計算、第一原理
計算等々。大体どれも同じようなものと思ってかまいません。但し、この中で”
第一原理”という言葉には特別な意味があります。
第一原理とは当の電子状態研究者の
間でも微妙に解釈が異なりますが、筆者の定義は”何ら実験結果を参照しない”
だけです。
因みに英語で電子状態計算分野での第一原理は、"first-principles"とか
"ab-initio"とか言われています。
厳密に言うと、”何ら実験結果を参照しない”という定義には問題がありま
す。電子状態計算を行なう場合、まず使用する計算コード、手法や(擬)ポテ
ンシャル、設定する計算条件などが正しいかどうかを判定するために簡単な系
の構造(対象とする物質の構成原子種毎の単体構造〔面心立方、体心立方〕)
の計算から始めます。この時、格子定数や体積弾性率などの計算を行ない、他
の理論計算値や実験値と比較しています。
この実験値との比較は、先の第一原理の定義に抵触しているとも言えます。
ただ現実問題として理論は理論計算の中で完全に閉じているわけではなく、一
番根源的な部分(ここでは格子定数などの物性値)に関しては、どこかで実験
事実との照合が必要になります。
第一原理の意味をここで補足するならば、(実際の)第一原理計算は、”研
究対象となる実際の系の実験結果に対して、理論計算結果を恣意的に合わせる
ようなことをしない。”ということです。
バンド計算屋の内情を言えば、実験には合わせているわけではないが、勘と
経験に依った(頼った)部分は現実には、その存在を完全払拭できてはいませ
ん。(^^;)
電子状態計算以外にバンド計算と言う言葉の方が、より一般的で良く聞くの
ではないかと思います。このバンドは(音楽のバンドとは一切関係ありません)
固体物理におけるバンド理論をその由来としています。
これはちゃんと説明しようとすると大変面倒(説明するための労力が多く必
要であり、かつ筆者自身にもちゃんと正しく説明できるか自信がない)なこと
になります。
できれば固体物理の教科書(「キッテルの固体物理学入門」など、物性論の
ものでも良い)を参照してもらえるとありがたいです。
非常に大まかに言えば、単独の原子の電子は1s軌道とか3p軌道とか言わ
れる原子軌道に電子が詰まっている状態であり、この個々の原子が集まって固
体構造(バルク構造)を作れば、原子間の電子同士が相互作用し、単独の原子
の局在した電子状態と異なるバンド(帯)構造なる電子状態を形成します。こ
のバンド構造から固体における結合状態(イオン結合、共有結合、金属結合等)
と電子状態(絶縁体、半導体、金属)との関係が定性的に説明することができ
ます。
バンド計算屋以外から最も良く聞く話が、”計算結果として出てくるバンド
構造(ディスパージョンとかE-k曲線、分散曲線、E-k分散、エネルギー分散、
バンド分散などともいう場合あり)がよくわからん。”です。
ここにバンド構造の例を示します(bandstructure.jp上の図
、png形式、90 kb)。古い(11/1、2010以前に使っていた)図(png形式、8 kb)。
もし絵が大変大きくなっていたら御容赦下さい。(2010年11月1日)
図をより分かり易くなるよう更新しました(ページアドレスも変更されていま
す)。
”よくわからん”というのは至極最もな話で、相当バンド計算の経験がない
限り、この手の特に先端的な研究領域で扱っているような系の複雑怪奇なバン
ドを見せられても、何をどう解釈すればよいのかさっぱりわからないと思いま
す。
実は、計算した当の本人も良くわかっていない場合も多く、他のバンド屋か
ら本人も気付かなかった、新しい知見や、場合によっては計算の間違いを指摘
されることがあります。
まず、バンド計算屋でない研究者がつまずくのは、絵の下のW、L、G(Γ)、
X、Kの記号の意味です(ここでGはΓ
のこと)。
このバンド構造は、実は逆格子空間(の第一ブリュアンゾーン)で計算された結果であ
り、逆空間の概念は実験でもX線回折などでは良くでてくる話です。先に述べ
たW、L等の記号は、このブリュアンゾーン内の対称性の良い点を表していま
す。
実際のバンド計算では、このブリュアンゾーン内をメッシュで分割して、各
点(メッシュの分割方法には等分割や、特殊点法などがあります)上で、バン
ド計算を行ないます。その中で特に対称性の良い点をΓ点とかX点とか言って
いるわけです。因みに、これらのメッシュ上の各点をk点と言います。
最も重要な点として挙げられるのが、Γ
点で、これはk = 0でのk点のことです。バンド構造の詳細は後述。
各結晶構造毎のブリュアンゾーンの構造でのk点の選び方、その呼び名など
は群論やX線回折などの専門書に載っています。バンド分散におけるk点の並
び順(対称線)の与え方に関しては、目的の物質(か目的のものと同じ対称性
を持った物質)を扱ったバンド計算関連論文などに載っているバンド分散
(E-k曲線)の図も参考となります。勿論、研究の目的に合った、或いは説明
し易い選び方が優先します。教科書としては例えば、"THE MATHEMATICAL
THEORY OF SYMMETRY IN SOLIDS", C. J. Bradley and A. P. Cracknell,
CLARENDON PRESS, Oxford 1972"や、以下に示す柳瀬先生の本などが挙げられ
ます。
- バンド構造(バンド分散)の例(図は全てpng画像)
- 【画像ファイルは、bandstructure.jp上にあります】
-
- 面心立方構造(FCC)←銀の場合
- 体心立方構造(BCC)←ナトリウムの場合
- 体心立方構造(BCC)←モリブデンの場合
- 単純立方構造(SC)←燐の場合
- 単純立方構造(SC)←チタン酸ストロンチウムの場合
- 六方晶構造1(HCP)←亜鉛(Zn)の場合
- 六方晶構造2(Hexagonal-BN)←六方晶窒化ホウ素(h-BN)の場合(P63/mmc)
- 六方晶構造3(Hexagonal-BN)←六方晶窒化ホウ素(h-BN)の場合(P63/mmc):h-BN(構造2)と異なったk点の並び方の例
- ウルツ鉱構造(Wurtzite)←ウルツ鉱型窒化ホウ素(w-BN)の場合
- 閃亜鉛鉱構造(Zinc Blende)←立方晶窒化ホウ素(c-BN)の場合
- 岩塩構造(Rock Salt)←岩塩(NaCl)の場合
- 岩塩構造(Rock Salt)←炭化チタンの場合
- ダイヤモンド構造(Diamond structure)←シリコンの場合
- ルチル構造(Rutile)←SiO2(Stishovite)の場合
- AlB2構造(Hexagonal ω)←MgB2の場合(P6/mmm)
- 以上のk点の並び、分散の表示の仕方は、一つの
例を示しただけであり、以上で示した図(の内容)と異なる表示例も多数存在
します。図の作成時期により、Γ点がGとして表記されているものが
あります。また必ずしも上記の表記が標準的であるこ
とを保証しません。どのような物性を知りたいかにより、k点の並び
方、選び方が異なることがあります。勿論、ここでは全ての結晶構造、物質の
場合を示していません。上記に示されていないものは、バンド構造図集
(上記で示した図は、これの抜粋)、他のオンライン上のサイト(”バンド構
造図集ページ”の下の方にリンクあり)、文献(バンド計算関連教科書、群論、固体物理の教科書、具体的な
論文等)などをご参照下さい。
この手のバンド構造の絵では大抵、系の対称性を考慮した計算がな
されています。つまり、バンド計算では群論も非常に大事になる場合が多数あ
ります。必ずしも対称性を考慮する必要のない場合もあります。表面系や液体
金属のように対称性が低い、或いは全くない系などがそれです。
結晶の対称性や群論に関して、柳瀬先生による”空間群のプログラム
(TSPACE)”、裳華房刊があります。非常に役に立ち、参考になると思います。
尚、柳瀬先生によるTSPACEページ
(2/25、2019、アドレス変更)にこの本の最新の正誤表や追加プログラムの記述があります。
また、同じく柳瀬先生による、「ブリルアン・ゾーンとは」、丸善もお薦め
です。
次にわからないのが、グラフ中の’うにょうにょ’した線(分散し
た線)です。これをバンド屋は何々バンドとか言っています。慣れたバンド屋
では、”ここらにあるのがd的なバンドで、7から8eVほど上にフェルミレ
ベル(フェルミ準位、フェルミエネルギーなどとも言う)がある。”などとの
たまいます。
尚、3次元のk空間上でのフェルミレベルの描く面がフェルミ面(Fermi surface)です。
この’うにょうにょ’した線1本が1つのバンドであり、スピンを考慮しな
い場合は電子が2個詰まることができます。
バンド計算では大抵、ユニットセル
(単位胞;平行六面体の箱の中に原子が入っている)を考え、そのセルに関し
てのみバンド計算を行なっています。これは現実問題としてアボガドロ数程度
の数の計算を行なうことはできないこから、周期的境界条件を使って単位胞
(ユニットセル)を考え(←完全結晶を想定している)、それをバンド計算す
ることで系(全体)の電子状態がわかります(或いはわかったようなふりをす
る)。
実はこの周期的境界条件を考慮することによって、ブロッホの定理が適用で
きることが、バンド計算におけるミソになっています。ブロッホの定理の詳細については固体物理の教科書を
参照してください。
同一の物質でも単位胞(ユニットセル)の”取り方”によってバンド構造は
一見異なって見えます。これは、単位胞(基本単位格子でない場合は、事実上
スーパーセルに相当)の取り方によって、ブリュアンゾーンの形が異なるため
バンド構造の描画段階(対称性の高いk点の名称が異なり、バンドの折り畳み
方も異なる)で差が出てくるためです。但し、これは見え方が異なるだけで、
選択した互いのセルの対称性の違いを考慮して折り畳み、折り開き(展開)を
行なえば、お互いが同一なバンド構造であることが示せます(示せるはず)。
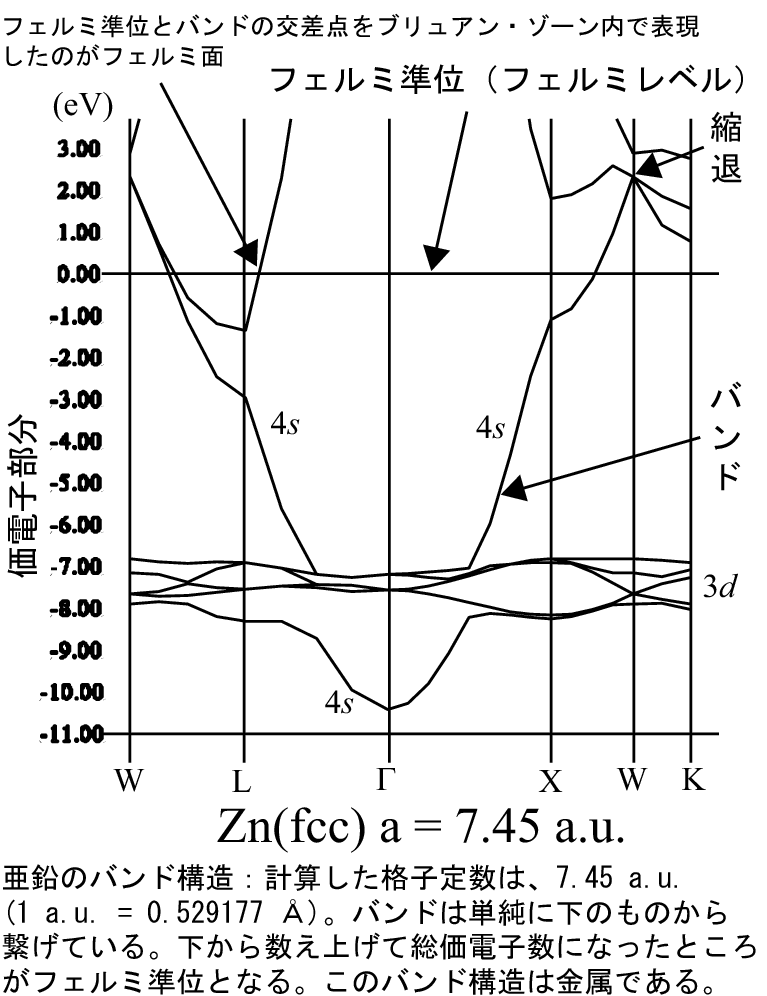
話が逸れてきたのでバンド構造の説明に戻ります。上記の絵は亜鉛の面心立
方構造(ユニットセルの中には1個の亜鉛原子があるだけ)のバンド構造です。
絵の縦軸は原子での電子軌道エネルギーに相当するもので、バルクのバンド
の準位またはエネルギーです。この絵での数字の単位はeVです。
ここで数字のゼロのところがフェルミレベル(フェルミ準位、フェルミエネ
ルギー、厳密ではないがフェルミ面と言ってしまうこともある)と言われるも
のです。数字ゼロのところに横棒が一本引いてあります。
(注意)バンド計算手法にも種類があり、筆者の行なっているバンド計算では、
価電子のみを考慮し(←擬ポテンシャ
ル法のため)、内殻の電子は一切計算していません(内殻電子を価電子と
して考慮する場合があります。例:浅い3d軌道も考慮したGaの
バンド構造[png形式、7 kb])。そのため、バンド構造は原則として全て
価電子部分のみの表示です。全電子手法を使えば、全ての電子軌道の
バンドを描画可能です。ただ、物性に関わるのは価電子部分とその近傍なので、
あまり深い軌道は描かないことが多いです。深い軌道のバンド(上の亜鉛で考
えれば、1s軌道や2s軌道)は、周囲の原子(とその原子内の電子)とほと
んど相互作用しないので、分散も弱くほとんど平坦なバンドとなります。先に
示した、Gaの浅い3d内殻軌道によるバンド(フェルミ準位以下、15 eV辺り
に位置している)も平坦(分散は非常に弱い)になっています。
このバンド計算でのフェルミレベルの定義は非常に単純です。ユニットセル
に亜鉛の原子が1個あり、その価電子の数は12個です。そして先に述べたよ
うに1本のバンドに2個ずつ電子を下のバンドから詰めて、扱っている全電子
数12個(この場合は、総価電子数←3dも価電子としている)に相当すると
ころをフェルミレベルとしています。固体物理における厳密な定義とは完全に
は符合しないものとなっています。あくまで計算上の定義ですが、実際の運用
上問題はほとんどありません。
もしバンドが極めて原子的ならば(例えば固体内の原子同士が非常に離れた
状態)、バンドはそれぞれ横一本の線になってしまいます(分散がない)。こ
の場合、電子は下から6本目の線まで全部詰まり、7本目以降は空のバンドと
なります。ここで系の総電子数は偶数なので問題ないのですが、電子数が奇数
の時は、ちょっと扱いが面倒になることがあります。
絵を見てわかるように、実際のバンドは相互作用によって分散を持ち、非常
に変化に富んだ一見すると複雑な構造になっています。従ってこの亜鉛のフェ
ルミレベル(バンドの下から数えて電子数が十二個目〔電子2個/1バンド〕
になる部分)も、絵にあるように、必ずしも下から6本目の線が詰まっている
というわけではなく、放物線的な4sバンド(4s軌道と言ってもかまわない)
をフェルミレベルが横切っています。(注)バンド構造として描画してい
るのは、全体の一部分(ブリュアン・ゾーン内の特定の線や点を選んでいる)
であることに注意して下さい。
ここで一つわかるのは、4sバンドは、比較的(s電子だから)自由電子的
であり、放物線的なバンド分散を持ちます。そしてフェルミレベルよ
り7ないし8eV下により局在した3dバンド(5本、電子10個分)があり
ます。d軌道はs軌道と比べて、局在しています。従ってバンド構造もあまり
広がったものではなく、構造の乏しいものになっています。(11/1、20
10)更新した図では、特定のバンドに対して、”4s”、”3d”と指し示
してあります。ただ本当は”4s的”、”3d的”であり、sとかdを完全に
分けて考えることは出来ません。どのバンドもs、p、d等が”適当”に混ざっ
ています。多くのバンド構造で、特定のバンドが主にs的か、p的か、d的か、
f的かをちょっと見ただけでは”はっきり”とは分からないと思います。目的
のバンドをs、p、d、fなどの成分毎に分離してそれらの寄与を調べる必要
があります。sとかpとかdとかに分けるのは、平面波基底を使った計算手法
の場合、ちょっと厄介となります。平面波が、s、p、dなどに簡単に分ける
ことが出来ないからです(勿論、対処方法はあります)。
単独の原子は、原子的な軌道準位を持っています。仮に最初非常に大きなユ
ニットセル内で各原子がお互い十分に離れているとすると、バルクとしてのバ
ンド構造もほとんど原子的な平坦(フラット)なバンド構造となりますが、ユ
ニットセルをだんだん縮めて(系を縮める)原子間距離が近付いてくれば、お
互いの原子の電子同士が強く相互作用するようになり、フラットであった原子
的な準位がだんだん複雑な構造(これがバンド〔構造〕の形成〔分散
すること〕であり、これが一般に言うバンド構造です)を持つようになります。
バンド構造図では一見一本に見える線(バンド)が、ある位置から2本や3
本に分かれている場合があります。これは、縮退していたバンドが、
ブリュアンゾーン上のある点(大抵対称性の良い点から)で分かれます(11/
1、2010に更新した亜鉛のバンド構造図で、縮退している部分を矢印
で示しました。ただ縮退しているバンドはそこだけではありません)。系
の持っている対称性から、どの点で縮退し、どの点で縮退が分かれる(解ける)
かが分りますが、完全に全て分るというわけではありません。また一見、1本
のみに見えるバンドが、実は2本のバンドが縮退していることもあります。
LiBCのバンド
構造(png形式、12 kb)では、Γ-A線上の占有された一番上のバンドは、
見たところ4重に縮退しているように見えます。ただ実際に当該する部分のエ
ネルギー固有値を調べてみると、Γ点上では2重縮退したエネルギー固有値が
非常に近い値で2つ存在する(合計で4本)ことが判明しました(A点で、そ
れらは4重に縮退します)。つまり2重縮退した2つのバンドが非常に接近し
て存在している訳です。
バンドの線同士が交差している場合がありますが、このバンドの絵は各k点
上のバンドを下から単純に繋げているだけです。実際は系の対称性によって交
差したりしなかったり(反発するようにみえる)します。これを実現するため
にはちゃんとした群論の手法を導入しなければなりません(参考ページ:非交差の規則)。
ただ、明らかに「この点(k点)では、縮退は起こらない、縮退は解けない」
と言う場合があり、バンド計算が正しいかどうかのチェックが行なえます。逆
にそのk点でのバンドの縮退数から、そのバンドの既約表現(→参考ページ)が判る場合もあります
(←多くの場合はそう簡単ではない)。k点上のバンドとそのバンドに対応す
る波動関数の既約表現を知ることは、通常はそう簡単なことではありません。
既約表現が分かると、いろいろと役に立ちます(例1:縮退数、例2:適合関
係〔←バンドの繋げ方〕や交差、非交差の判定、例3:双極子遷移での選択則
に基づく、遷移許容、禁制の判定)。
これらはかなりバンド計算やバンド構造、群論等に詳しくないと分らない
ので、学会発表の段階でバンド構造の致命的な間違いを指摘されることもあり
ます(”そのバンドはその系の対称性から、そのX点上で2重縮退は起こらな
い。”などと言われて大恥をかくことがあります)。
このバンド構造図(結果)がどのような実験結果と比較し得るかと言うと、
まずUPS、XPS、ARUPS、ARPES等の分光実験が挙げられます。実験、理論相方と
も間違いがなく、十分精度に留意すれば、お互いに十分比較しうるものです。
特に最近(2006年頃)、角度分解光電子分光(ARPES)の精度が大幅に向
上(1 meVのオーダー、場合によってはそれ以下←バンド計算結果
との詳細な比較が可能)し詳細なバンド構造が実験的に得られるようになっ
ています(光電子分光実験の研究室の例:東北大学理学部、光電子固体物性研
究室〔高橋研究室〕、ARPESカレンダーが素晴らしい)。ARPES実験の結果と第
一原理バンド計算で得られるバンド構造との直接比較が可能となっています。
他の例として私事ですがSi(001)表面にアルカリ金属が吸着した場合
の飽和吸着量に関してARUPSの実験(東北大学の河野先生のグループによる)
から、吸着量が飽和している時の表面電子状態は半導体的であるという指摘
(当時、飽和吸着量に関しては、2×1表面にアルカリ原子が1個着くか、2
個着くかで論争があった。実を言えば、いまだに完全な決着はついていないよ
うだが、、、)がありました。
バンド計算してみると、表面電子状態が半導体になるのは、シリコン表面上
にアルカリ原子が2個ついた場合であることがわかりました。そのため我々は
飽和吸着量がθ=1(つまり2×1表面に2個)と結論したことがあります。
(これは研究自身は筆者が無機材研へ入所する前の研究です(参考文献:
Phys. Rev. B45, 3469(1992))。
加えて、我々のシリコン表面の計算によるバンド構造とARUPS実験の結果は
大変良い一致を見ました。また逆光電子分光とも大変良く一致していました。
逆光電子分光はフェルミレベルより上のバンドに対応しますが、実は通常バ
ンド計算では密度汎関数理論〔一種の
変分計算〕をもとにしており、この理論は基底状態に関してのみ正しいことが
証明されています。従って、フェルミレベルより上のバンドは励起状態に相当
するので、本当に正しい計算を行なっている保証は厳密にはありません。ただ、
経験的にはそう悪くはない結果が得られることがわかっています。実際、我々
の計算と逆光電子分光実験との一致はきわめて良いです(合わせるためにバン
ドの位置をずらしたりしてはいる。←シザーハンド法)。ただしいつ
でも良いという保証は全くありません。
(状態密度)
このバンド構造の絵で、これを横方向に足し上げていくと(つまりk点で積
分すると←単に横方向だけでなく、BZ内全体で足し上げる)、系の状態密度が得られます。つまり各
エネルギー毎の状態数が得られます。この計算結果はフォトエミッション
(Photo emission)の実験結果と比較できます。但し、理論計算ではやたら詳細
な構造が出てきますが、実験結果はより大まかなぬらっとした構造しか出てき
ません。従って、あまり詳細な部分の議論は不可能です(Spring-8のような高
輝度光源を使えば、実験の精度〔解像度〕が非常に良くなると期待されていま
す)。
密度汎関数法をもとにしたバンド計算での温度は絶対零度であり、計算され
る対象も多くの場合理想的な条件(普通、完全結晶を考え現実に存在するはず
の不純物や欠陥の効果を考慮していない)が課されます。
一方、実験は有限の温度のもとで行なわれ、不純物、欠陥、外部からのノイ
ズ等いろいろな効果が結果に入り込んでしまいます。あとおそらくエネルギー
に関する解像度の問題もあると思われます。バンド計算では非常に細かい刻み
(意味があるかどうかは別として)での表現が可能です。
状態密度をエネルギーに関してフェルミレベルまで足していくと、系(ユニッ
トセル内)の全電子数になります。今の場合、ユニットセル中にある亜鉛原子
数は1個なので、全電子数は12個となります。任意のエネルギーまで状態密
度を足し上げた量を状態数(または積分状態密度)と言います。
以上では、亜鉛を参考例として挙げましたが、これは金属のバンド構造の一
例でしかありません。他にもギャップ(バンドギャップ、禁止帯)の存在する
半導体や絶縁体にも当然バンド構造が存在します(密度汎関数理論+局所密度
近似の範疇でのバンドギャップの過小評価に
ついては後述)。
(非周期的な系にバンド構造は存在するか?)
非周期的な場合はどうするのか(ギクリ!)と言われると、バンド計算は基
本的に周期的な場合を大前提としているため、そのままでは非周期的な場合
(表面系、界面系のような半無限なものや、アモルファス(硝子)、液体金属、
水などの液体、準結晶、不純物、欠陥などを扱うのも苦手)を扱うことはでき
ません。
このような周期的境界条件を課すことが出来ない系であっても、当然電子状
態が存在するはずですが、それをバンド構造として視覚的に表現することは困
難と言えます。それはバンド理論、バンド計算は基本的に周期的境界条件下に
あることが前提となって成り立っているからです。非周期系に対しては無限大
の大きさのユニットセルを考えれば、バンド(よりかは状態密度)としての記
述が可能と思われます。ただこの場合k点は実質上Γ点のみで記述できます
(←逆空間は無限小=Γ点〔k = 0〕。このためバンド構造と言うより、
状態密度での記述が自然となる)。
このような非周期的な系を扱う便法の一つとして、スーパーセル法があります。これはユニッ
トセルよりもずっと大きなセルを考える(バンド計算では数十から数百原子の
規模)というものです。このスーパーセルも隣接するスーパーセル同士はやは
り依然として周期的ですが、セルが大きな分、非周期的な効果をある程度考慮
することができます(非周期的な場合のバンドの記
述)。一方、準結晶に関してはそれに類似する近似結晶を使ってバンド計
算が行なわれたりします。実空間法を
使う手もあります。
(直接ギャップ、間接ギャップ)
半導体や絶縁体のようなギャップの存在する物質では、そのギャップが直接
型か間接型かは大変重要な意味を持ちます。
バンド計算の結果として描かれるバンド構造は、h-BNを例にすると、
そのバンド構造は次のように描かれます。
h-BNバンド1(k点の横座標幅が狭い方、png画像、6.8 kB)、
h-BNバンド2(k点の横座標幅が広い方、png画像、7 kB)と2つ
のk点の取り方でのバンド構造を比較してみます。見てすぐ分かるように、取
るべきk点の範囲の違いでバンド構造の見え方は大分異なります。計算上、
h-BNは間接ギャップ型であることが分かっていますが、狭いバンドで
は一見、M-Kの間接ギャップに見えます。しかし広いバンドで見ると、実際は、
M-Hの間接バンドギャップになっています(←こっちが正しい)。更に、これ
は限定された代表的なk点のみからなる線上のバンドしか見ていないので、そ
の他の一般k点でのバンド構造が表現されていません。実は、この表現されて
いない部分で直接ギャップ型になっている可能性は完全に排除できません。従っ
て本来なら、それら一般のk点まで含めた、計算上得られるk点全てに関して
直接か間接かを判定する必要があります。
因みに、一般のk点まで考慮しても、h-BNのバンドギャップは、M-H
の間接バンドギャップとなります。但し、これが実験結果と符合するかどうか
はまた別問題です。
(参考ページ)
筆者が計算した系のバンド構造の結果をpng形式の画像として網羅した”非
周期的バンド構造図集”の[ページ]
第一原理電子状態計算と言っても、実はいくつかの種類がありそれぞれ長所
短所があります。
分け方にもよりますが多分種類としては大きく2つに分けることができます。
これは計算で扱うべきポテンシャルの種類によって分けられます(計算の対象
となる原子の内殻電子を考慮するか、しないかによって分けられるとも言える)。
一つは、all-electron法(全電子法)
であり、いま一つは擬ポテンシャル法
です。因みに筆者は後者の方法のみ経験があります。これら両者の違いは、
all-electron法では計算対象となる原子中の電子は内殻も含めて一応全て扱う
のに対し、擬ポテンシャル法は原子の価電子しか考えないというところにあり
ます。
All-electron法 [先頭へ]
all-electron法には、LMTO、APW(LAPWやFLAPWも含める)、KKRなどの方法
があります[参考ページ]。
LMTO法:Linear Muffin-tin Orbital法(線形化されたマッフィンティンポ
テンシャルの軌道による方法)
APW法 :Augument Plane Wave法(補強された平面波による方法)
KKR法 :Koringa-Kohn-Rostoker法(3人の人名の頭文字)
筆者はall-electron法の計算の経験がほとんどなく、難しい説明にもなり
(本当は筆者本人が良く分っていない)ますので、詳細な説明は省略します。
多分、上記方法を使用しなければならないということにでもならない限り、詳
細を知っておく必要性は全くないと思われます。
大事なこととしては、精度的にはAPW法(特にその中でFLAPW法)が最も精度
の高い計算ができます。(APW法とKKR法は精度的には等価です、最近full
potential〔FL〕なKKR法も出現しています。ただバンド計算屋の中では何故か
(FL)APWを使用しているグループの方がずっと多いです。
LMTO法は先のAPW法やKKR法と比べると精度的にやや劣りますが、非常に高速
に計算を行なうことができます。最近、LMTO法でもfull potentialのものが出
現し精度的な部分もある程度改善しつつあります。
特に、Physical Review等の雑誌を見ると、上記all-electron計算で最も良
く見るのは、LMTO法や(FL)APW法、これらと比べてKKR法は少なめとなっていま
す。他にも見かける全電子計算手法として、NMTO、EMTO、ASW(←LMTOの親戚
筋と言える手法)などがあります。
LMTO法はバンド計算法としては比較的お手軽で(計算が速く、消費メモリー
も少ないです。このためワークステーションや最近のハイエンドパソコン上で
計算が十分行なえます)、使用ユーザーは多数かつ多岐(実験研究者の中にも
LMTO法を使用している場合があります)に渡ります。
たまに偽ポテンシャルと書かれている場合もありますが、大低擬
ポテンシャルと書きます。
これは本ウェブページサイトにある擬ポテンシャルデータベースNCPS9
5(97、2K)の説明を参照して
下さい。そこに詳しい説明があります。ここで簡単に説明すると、通常固体物
理物理で重要な物性の多くは、原子の価電子の部分からの寄与が大部分であり、
内殻の電子からの効果はほぼ完全に無視できるとして、原子の価電子の部分だ
けで作られたポテンシャルを”擬ポテンシャル”と言っています。
1970年代まで、擬ポテンシャルは経験的に求め(第一原理ではなかった)
ていましたが、1979年Hamman、Schlüter、Chiangによって第一原理
擬ポテンシャルである、ノルム保存擬ポテンシャル(或いは、ノルム保存型擬
ポテンシャル)が登場しました。筆者が使用しているのも、このノルム保存擬
ポテンシャルです。
このノルム保存擬ポテンシャルにも、よりソフト化したバージョン(ソフト
化=より滑らかにすること=基底関数を減らせる=バンド計算が楽になる。た
だ下手にソフト化すると計算間違いの原因になることもあります)や、ノ
ルム保存条件をはずしてよりソフト化した擬ポテンシャル(ウルトラソフ
ト擬ポテンシャル、或いは超ソフト擬ポテンシャルなどと言う)などもありま
す。
そしてこの擬ポテンシャルをもとに、大抵基底関数に平面波を用いた第一原
理擬ポテンシャル電子状態(バンド)計算が行なわれます。
基底関数に平面波を使用すると、all-electron法と比べてずっと容易に原子
間に働く力や、系に懸かる圧力(ストレス)の計算ができます。
これを応用すると、電子状態計算と分子動力学計算をドッキングさせることが
できます。これがカー・パリネロ法(Car-Parrinello法≒第一原理分子動力学
手法)です。
これは1985年当時イタリアのトリエステにいたカーとパリネロが発表し
た方法です。既に20年が経った手法ですが、基本的には現在(2006年)
でもノルム保存擬ポテンシャルと平面波を使った方法が主流です。そのため項
目としては前述の擬ポテンシャル計算の範疇に入ります。
この方法は2つの点で大変重要なことが行なわれています。一つはハミルト
ニアンの対角化を陽に行なわないで固有値問題を解いていること、もう一つは
同時に系の原子も動かして(分子動力学)いることです。
前者は、系の波動関数と原子の座標をいずれも動力学的に解けるものとみな
し、波動関数を仮想的な質量をもった粒子と考えてこれを分子動力学的手法で
解いてしまおうとしたのがカーとパリネロのオリジナルな考えです。これによ
り大変な計算量とメモリーを必要とした対角化の手法を用いないで済むことに
なり、電子状態計算で必要な計算量とメモリーが大幅に削減することができま
した。
更に、系の原子も同時に動力学的に扱うので、構造の最適化が行なえ同時に
その電子状態も求めることができます。構造の最適化における安定構造の探索
は必ずしも大局的(グローバル)な探索が行なわれる訳ではなく、現実には局
所安定構造の探索が精一杯と言ったところです。
一方原子を動かす毎に電子状態計算を行なうので、ポテンシャルが毎回更新
されます。これまでの古典的な分子動力学法では構造の最適化中、ポテンシャ
ルが更新されることがない分、カー・パリネロ法ではより精度の高い構造最適
化が行なえます。
ただし、その分カー・パリネロ法では、扱える系の規模が古典的な分子動力
学法よりずっと小さくなります。これはカー・パリネロ法では原子を動かす毎
に電子状態計算を繰り返しますが、この電子状態計算に莫大な時間を要するた
めです。大雑把ですが計算全体の99%はこの電子状態計算に費やされてしま
います。
従って、カー・パリネロ法の扱える系の大きさは古典的な分子動力学法が数
万から数百万の原子数で計算できるのに対して、せいぜい100個位です(1
990年代)。最も良い条件(含む計算機資源の質と量)なら100
0〜数千原子程度までできます。
カー・パリネロ法が出現してから20年以上経ち、カー・パリネロ法も幾つ
かの点で、改良、進歩がみ見られました。その詳細は省略しますが、以下にい
くつか挙げてみます。
(1)動力学手法(波動関数更新手法)の改良 ⇒ 最急降下法や現在最も効率の良い共役勾配法の導入(更にもっと効率の良い
方法〔RMM-DIIS法〕も導入されている)
(2)all-electron法に対するカー・パリネロ的手法の導入(参A. R. Williams)
(3)並列計算機への応用(計算手法のパラレ
ル化)
(4)様々なダイナミックス(局所的な構造最適化を越える試み)手法の導
入(例:"Blue moon"、"Metadynamics"等)。
因みに、カー・パリネロ法の呼び方としては、他に第一原理分子動力学法、
非経験的分子動力学法、量子分子動力学法、ab-initio分子動力学法などとも
言われます。厳密にはそれぞれ意味合いが微妙に異なりますが、筆者としては
どれも少なくとも広い意味でのカー・パリネロ法の範疇に入ると思っています。
対象を第一原理電子状態計算(上記バンド計算法で説明したもの)に限定し
て、一体近似によるバンド計算はどこ
まで正しい結果を出すことができるかをここでは議論して行きたいと思います。
この場合、まずバンド計算ではどのような物理量が計算できるかについて説
明する必要があるかと思います。以下にそれを列挙してみます。
- これまでに出てきたバンド構造(*)
- 電荷密度(*)
- 系の全エネルギー(*)
- 系のエンタルピー(*、圧力の計算が必要)
- 系の自由エネルギー(?、有限温度への拡張が必要)
- 局所的な安定構造(*、要カー・パリネロ法)
- 格子定数と体積弾性率(*)
- ストレス(圧力)(*、1)
- 磁気モーメント(*)
- 結合エネルギー(*、2)
- 凝集エネルギー(@)(LDA)
- 凝集エネルギー(@)(GGA、LDAより精度が向上)
- フォノン振動数(@)
- フォノン状態密度(@)
- 状態密度(*)
- 仕事関数(表面系)(*)
- 各種弾性定数(@、3)
- 誘電関数 (?、4、WIEN2Kなどでは可能)
- 誘電率(?、4、WIEN2Kなどでは可能)
- グルナイセン定数(?)
- 超伝導転移温度(?、5)
- コンプトンプロファイルや陽電子消滅→ 運動量密度(?)
- フェルミ面(ドハース・ファンアルフェン効果)(?)
- 超微細構造定数(?)
- 熱伝導率、ゼーベック系数(?)
- その他いろいろ(?、6)
説明:(*)は筆者がバンド計算で出すことができる物理量を意味します。
(@)はその気になれば出せないことはない物理量です。但し、筆者は求めた
経験がないか、あっても非常に昔にやったことがちょっとだけあるという程度
です。(?)はバンド計算で求めることはできるが、筆者の手持ちの手法だけ
ではすぐには求めることができない(つまり、方法的に大幅な改良が必要な)
ものです。
(*、1):ストレスの計算から系の形(セルの形)そのものの構造最適化
が可能です。慎重に計算すれば(大規模な計算になりますが)構造相転移のシ
ミュレートも可能ではある思います(実際に他のグループで計算例あり。→
[参照])。
(*、2):例えば、シリコン表面に吸着したアルカリ原子の吸着エネルギー
(結合エネルギーに相当)を求めることが可能です。またバルクの構造の全エ
ネルギーE(バルク)と、孤立原子の全エネルギーE(アトム)がわかれば、
それらの引き算〔E(バルク)−N×E(アトム):ユニットセル内にN個の
原子が存在する場合〕から凝集エネルギーが求められます。結合エネルギー、
凝集エネルギーはGGAの導入によっ
て、計算値の精度が大分改善されます。参考:全エネルギーの比較
(*、3):前述のストレスの結果を利用していろいろな弾性定数が求めら
れます。最近はDFPT手法を使って計算
することも出来る。
(*、4):WIEN2Kパッケージでは
誘電関数を求めることが可能になっていて、比較的簡単に求めることができる
ようになっています(他のコード、計算手法でも求めることが出来るものがあ
ります)。
(*、5):フォノン振動数を計算して得られた結果を使って、超伝導転移
温度を求める式から超伝導転移温度を求めることが可能(この場合、第一原理
的には求められないパラメータが存在)。従来は、調和近似を前提として原子
を変位させて得られる力からフォノンの振動数を求めていました。Γ点以外の
k点でのフォノン振動数を求めるにはスーパー
セルを考える必要があり、膨大な計算量が必要となります。最近は線形応
答理論を使った方法でフォノン振動数、フォノン状態密度等をこの従来の方法
より、もっと容易に求めることも可能になっています。擬ポテンシャル+平面
波のバンド計算でも可能(線形応答を使ったものとしては、X. Gonze等による
ABINIT[コード]などがあります)、求
めるためには通常のバンド計算手法の大幅な改良と拡張が必要です。
(例)2001年初頭に発見された、
MgB2(転移温度:39 K)に対し、バンド計算から求めた転移温度
は、20 〜 20数Kという値となる(これを良い精度とみなすか、そうとらない
かは難しいところ←筆者の感覚では”まあそれなりに良く当たっている”と思
う)。
(*、6):その他にも計算可能な物理量があると思いますが、いますぐに
は思いつかないので、おいおい出していきたいと思います。
では実際どのくらいの精度(信用度)で、実験結果と比較できるのでしょう
か。以下に、先に挙げたリストを若干補足して再び示します。
- 前に出てきたバンド構造(*)_かなり信頼できる場合もあり(ウソもある)。
- 電荷密度(*)________かなり信頼できる。
- 系の全エネルギー(*)____相対値としては非常に信頼できる。
- 系のエンタルピー(*)____相対値としては信頼できる。
- 系の自由エネルギー(*)___相対値としてはある程度信頼できる(?、有限温度への拡張とその精度の問題)。
- 局所的な安定構造(要カー・パリネロ法)(*) かなり信頼できる。
- 格子定数と体積弾性率(*)__実験との差は格子定数で1%、体積弾性率で10%
- ストレス(圧力)(*、1)__まあ信頼できる。
- 磁気モーメント(*)_____ある程度信頼できる。
- 結合エネルギー(*、2)___ある程度信頼できる。
- 凝集エネルギー(@)_____あまり当てにならない(LDA)。
- 凝集エネルギー(@)_____ある程度信頼できる(GGA)。
- フォノン振動数(@)_____かなり信頼できる。
- フォノン状態密度(@)____まあ信頼できる。
- 状態密度(@)________ある程度信頼できる。
- 仕事関数(表面系)(@)___ある程度信頼できる。
- 各種弾性定数(@、3)____ある程度信頼できる。
- 誘電関数(?、4)______ある程度信頼できる。
- 誘電率(?、4)_______ある程度信頼できる。
- グルナイセン定数(?)____ある程度信頼できる。
- 超伝導転移温度(?、5)___計算は可能(任意パラメータ〔μパラメータ〕あり)(←第一原理的に求めるアプローチあり)。
- コンプトンプロファイルや陽電子消滅→ 運動量密度(?) ある程度信頼できる。
- フェルミ面(ドハース・ファンアルフェン効果) ある程度信頼できる。
- 超微細構造定数(?)_____計算は可能
- 熱伝導率、ゼーベック系数(?) 計算は可能(緩和時間τの扱いが難しい)
- その他いろいろ(?、6)
計算結果に対する信頼度について寸評してみました。理論の立場からは’か
なり’という言葉はあいまいであまり使いたくなかったのですが、他に良い言
い方がなかったので使用しました。この評は筆者の独断と偏見も含ま
れています(そんなことはないという御指摘があると嬉しいです)。
信頼度の順番として、一番信用できるものから、”かなり信頼できる”、”
まあ信頼できる”、”ある程度信頼できる”、”計算は可能”、”あまり当て
にならない”、となります。あと”?”は筆者の知識不足から詳細不明のもの
です。
格子定数に関しては、標準的に実験との誤差が1%以内になることがバンド
計算の世界では常識になっています。しかし、現実には系によっては1%以内
というのが難しい場合もあり、悪くとも2ないし3%が許容範囲としての限界
と思われます。バンド計算で求まった格子定数に3%以上の実験との差がある
場合は、(実験値が正しいとすれば)バンド計算結果に精度上の何らかの問題
があると思われます。
この”何らかの問題”は2つ考えられ、1つはバンド計算そのものの限界で
正しい格子定数が得られない場合、いま1つは計算上の間違いなどで格子定数
が出ない場合とがあります。例えば擬ポテンシャルによるバンド計算では作成
したポテンシャルが良くないと格子定数がまともに出ない場合があります。こ
れは計算上の間違いと言えますが、アルカリ金属の場合のように浅い内殻電子
を考慮しないと、格子定数が数%短めにでる場合もあります。これは間違いと
言うよりはその計算そのものの限界であると言えます。アルカリ金属の格子定
数過小評価の問題は、内殻補正を考慮すればある程度改善します。
全般に構造に関する計算は比較的信頼性が高く、構造の最適化によって局所
的な安定構造を探索した結果は、実験結果と十分比較しうるものになっていま
す。
例えば、シリコン表面に吸着したアルカリ原子の吸着位置や、シリコン
〔Si(001)〕表面のダイマー構造が非対称か対称か、シリコン表面上のダイマー
構造は非対称だが、ダイヤモンド表面のダイマーは対称であるなどの議論では、
非常に厳密な議論を行なうことが可能です。実は、シリコン表面のダイマー構
造の話はそう簡単ではないことが分かっていますが、詳細はここではご勘弁下
さい。他にもバルク中の不純物の局所的な安定位置、高圧下での安定構造の候
補選びなどでもかなり信頼できる結果が得られる場合があります。ただ求めら
れるのは局所安定構造である場合が多く、また扱える系の規模もユニットセル
にせいぜい100個程度がいいところなので、本当の意味での新物質の探索な
どが自在にできるという訳では決してありません。
このような構造間での安定性を議論するときに使われる計算結果が全エネル
ギーです。全エネルギーは相対的なものとして考えるなら、十分精度に気を付
ければ数meV(温度にして数十K)のエネルギー差の議論が可能です。実際
問題としては”A系とB系のエネルギー差が、全体で数十meVあり、このた
めA系の方が安定だ。”というようなバンド計算屋の主張にはそれなりの信頼
性があります。
また、同じ物質の異なる相同士での圧力による構造相転移の転移圧力は、そ
れぞれの全エネルギー‐体積(Etot - V)の曲線同士の共通接線
から求めることが可能です(温度は絶対零度が想定されていることに注意)。
勿論、これは負の傾きの共通接線が引ける場合に成り立ちます。圧力をPとす
ると、P = - ∂Etot/∂Ω(Ω:系の体積。この場合、単位胞の体
積)から求まります。圧力やストレス
に関しては、ストレス関係論文をご参照
下さい。
一方、等方的な圧力を印加する場合には、エンタルピー(H = E + PV、H:
エンタルピー、E:全エネルギー〔=内部エネルギーと考えて良い〕、P:圧力、
V:系の体積)がエネルギー安定の比較に使用されることがあります。上に述
べた共通接線は等エンタルビー線を意味している(以下の図参照←png形式、
12 kb。図ではα、β、γの3つの相の全エネルギー - 体積の曲線を描いてい
る。必ずしもウェブページ上の文章の説明と整合したものではないことに注意)。
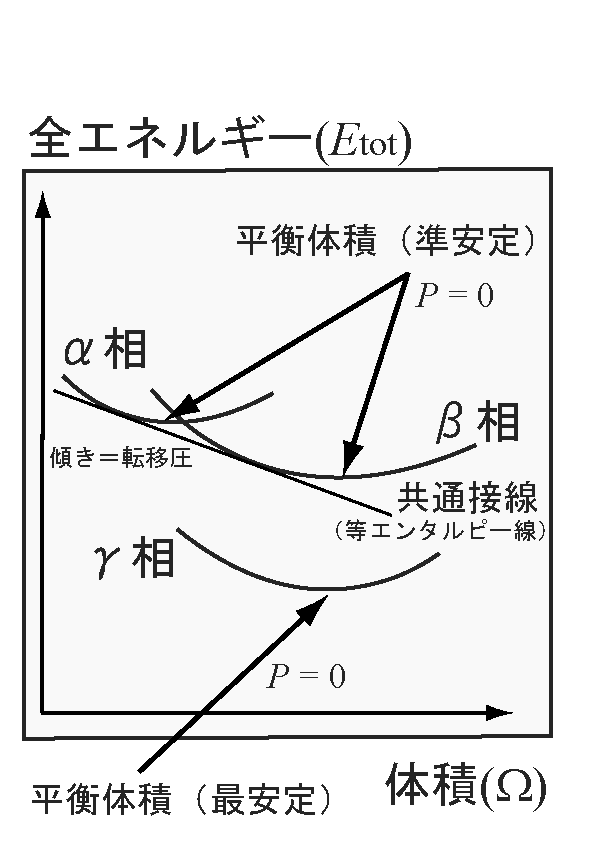
ただし、この時A系とB系で、原子の種類とそれぞれの数(構成比)が一致
していないといけません。そうでないと相対的な引き算ができません。(本当
はユニットセルの大きさや形に関する制約〔つまり系の対称性に対する扱いの
問題等〕も必要なのですが、ここでは難しくなるのでこれ以上議論しません。)
特に、ユニットセル内の原子の数、構成比が異なったり、計算条件が異なる
(ブリュアンゾーン内のk点数が異なる、基底関数の数が異なる等)場合には、
ほとんどお互いの全エネルギーを比較することに意味がない(うまく帳尻を合
わせても精度が出ない)と言えます。
勿論、凝集エネルギーとして考える場合は、比較は可能となります。
バンド構造は役に立つ時と立たない時があります。実は、バンド計算では厳
密に求めるのが大変厄介(と言うかほとんど不可能)な電子の交換・相関相互
作用部分(含む多体効果)に対して局所密度
近似(一電子近似も関連)という手段を用いて対応している場合が普通で、
この近似を用いた場合しばしばバンド構造が正しく求められないという事態が
起こります。正しくない結果を与える場合として、半導体(絶縁体)のバ
ンドギャップがあります。ギャップは実験値と比
べてまともな値が出ません。大体実験値の半分〜6、7割程度の値し
か出ません。また扱う系によっては本当は絶縁体(半導体)なのに計算してみ
ると金属になってしまうことがあります。バンド構造を見て、安易にこの系は
金属であると断ずることができない場合があります(ただ、注意しなければな
らない系はある程度絞ることができる〔例として挙げれば強相関系が該当〕の
で、どのような場合に対しても神経質になる必要はありません)[参考ページ]。
局所密度近似に対する補正を導入すれ
ば先の問題はある程度解決しますが、まだ決定的な解決法は今のところありま
せん。学会発表で、何の補正も解決策も講じないで半導体(絶縁体)のバンド
ギャップが正しく求められているような第一原理電子状態計算があったら、そ
の計算は非常に怪しいと思ってもらってかまいません(非第一原理に
よるバンド計算ではギャップの値が正しく出でていることもあるが、それはむ
しろギャップが正しく出るようにパラメータ調整を行なっていると考えられま
す)。
バンド計算も日進月歩で進歩しており、3年前の最新のアルゴリズムがあっ
とい間に陳腐化してしまう場合もあります。精度上の改善も着々と進んではい
ます。しかし、それでもまだ依然としてバンド計算にはいくつかの限界が存在
します。
- バンド計算は絶対零度のもとで計算されている(有限温度に対応していない)。
- イオン散乱実験で出てくるような、(任意の)イオン化した原子を扱うことは基本的に不可能。
- 既に局所密度近似は限界か?
- 電子の多体効果を直接的に扱えない(一体近似のため)。
- 強相関系では通常無力(例:高温超伝導、遷移金属酸化物、重い電子系など)。
- モット転移をバンド計算(バンド理論)では説明できない。
- 励起状態を厳密には扱えない(密度汎関数法は基底状態に対してのみ保証)。
- 非断熱過程(原子核の動きに電子が追随できない)を記述できない。
- 本当の意味での非周期系を扱うことが難しい(実空間法は除く)。
- その他(沢山^^;)
上記事項が全て不可能と言うわけではなく、方法の改良、拡張によって上記
問題(困難)を解決しようとする取り組みや努力が行なわれていて、ある程度
の成果を挙げている例もあります。しかしながら、ごく一般的にはバンド計算
で出来ないことは非常に多いと言えます。
非常に曖昧な(理論なのに)表現となりますが、(第一原理)バンド計算は、
過大に評価(期待)されている場合と過小に評価されている場合の二通りに分
れていると筆者は強く感じます。適切な評価がなされている場合があまりない
と筆者個人は思っています。適切に評価してもらうためにこれを書いていると
も言えます)。
これに関していくつかのパターンを以下に示します。
- 誰かバンド屋さんに頼む(共同研究)。
- 出来合いの市販ソフトを使用する(要購入)。
- 無償で公開されているソフトを使用する。
- 従来型バンド計算プログラムをゼロから自力で作るのはやめる。
- 外注でバンド計算プログラムを作ってもらう(有償)。
- 外注で計算してもらう(当然、有償)。
- ワークショップ、勉強会等への参加
- オンライン(掲示板、メイリングリスト←普通、参加申し込みする必要がある)で尋ねる。
- 諦める^^;
まず、上記リストの各項目について考察してみます。リスト1は最も簡単で、
確実な選択と言えます。但し、相手のバンド屋さんの力量を見極めておく必要
があり、選ぶ相手には十分な注意、検討が必要です。選択を誤ると間違ったバ
ンド計算結果を掴まされる場合があります。またこれは大抵所属機関が異なる
相手との共同研究となるので、お互い意思の疎通を良く図っておかないと思惑
通りに研究が進展しない可能性があります。また面倒な事務手続き(共同研究
契約等)が必要になる場合があります。
リスト2は、どこか市販されているバンド計算ソフトを購入して使用すると
いうものです。市販されているソフトなので、正規に購入すればマニュアルや
バージョンアップ、技術上の支援等のサービスが受けられます。バージョンアッ
プや支援、保守にはパッケージ購入とは別途有償な場合があるかもしれません。
事前によく調べておくことをお薦めします。また年度毎に保守契約(有償)を
しないと各種サービスが継続して受けられない場合もあります。
マニュアル等が完備されているとは言え、これらのソフトを運用して、(正
しい)結果を出すためには、それなりの努力と知識(量子力学や群論を知って
いると好都合)が必要であると言えます。また計算機(ワークステーションや
利用可能ならスーパーコンピューター)が楽に使えることも必要です。当然、
その計算機のOSやバンド計算を記述するプログラム言語(大抵はFORTR
AN、最近はC++も多い)、並列化技法などに対しての深い造詣があること
が望まれます。
市販されているパッケージについては、筆者用語集ページの[実践編]をご参照下さい。
この手のソフトは大体全体で数万行から数十万行にも及ぶ大規模なもので、
数年以上の期間をかけて作られたものです。それには莫大な労力と頭脳が注が
れています。従って一見法外な値段のように見えても実は妥当な場合が多いと
言えます。個人的には1つのバンド計算〔第一原理電子状態計算用〕ソフトを
作ることは一つの実験装置を作るのと同じと思います。特に、日本ではソ
フトに対する評価が大変低いと筆者は考えます。
リスト3は、状況としてはリスト2に酷似しますが、無償ソフトの場合マニュ
アル(ドキュメント、取り扱い説明)やバージョンアップなどのサービスが無
い、或いは十分ではない場合があります。またソフトそのものの機能も市販品
より劣る場合があります。また研究または教育機関に対してのみ無償という場
合もあります。この場合、ソフトの内容はリスト2に準じます。
無償で配布されているものとしては、第一原理分子動力学計算プログラムと
してCAMP-Atami(純国産、当該[ページ]←現在繋がっていない)がありま
す。その他、国内外で無償またはそれに準ずる公開ソフトが複数([用語集]参照)あります。これらの詳細(有償か
無償か、入手方法、ライセンス等)は上記用語集から辿る(リンクあり)ので、
リンク先の説明、ドキュメント等をご参照下さい。
最近(2012年現在)は、国内でもCMDワークショップ(とその関連グルー
プ、研究室)や「ノートパソコンで出来る原子レベルのシミュレーション入門
講習会」のような、具体的な第一原理計算コードの使用を前提とした講習会、
セミナー等が定期的に開催されています。
(敬意を払う)
これらのソフトも無償のものでも、大変な労力と知的な資源が投入されてい
る場合が多く、使用するに当ってはソフト製作者の意図を尊重し、その指示に
従ってください(少なくともパッケージ使用に関する説明ファイル位は添付し
てあるはず)。
また公開していないバンド計算による研究を行なっている組織、グループか
らプログラム(その組織、グループ独自のもの)を無償で提供してもらうとい
う手もあります。この場合はリスト1の変則的な場合としてとらえることがで
き、共同研究という形で話が進んでいくものが多いと思われます。また提供し
てくれた機関からの有形、無形の支援を受けられるという利点もありますが、
リスト1でも書いたように共同研究がうまくいかないと破綻してしまう場合が
あります。
(リスト4について、2/1、2002)
(2/1、2002)”作る”から”作るのをやめる”に変更しました。
バンド計算プログラムを作ることは、相当バンド計算に関して知識がないと
不可能です。大抵はバンド計算を行なっている研究室やグループに(学生など
の身分で)所属し、何年も丁稚奉公(?)して、その過程でバンド計算プログ
ラムを作ったりする場合が多いと思います(一番最初のバンド計算プログラム
はという質問は却下:-))。
全くの素人が1、2カ月程度で本格的なバンド計算プログラムを作成するこ
とは不可能と言っても良く、普通、何の知識も元となるプログラムもない状態
から全くの独学かつ1人でバンド計算プログラムを作り始めれば、おそらくま
ともに結果が出せるようになるまで2、3年は必要と思われます。
(↓この有利さは既に大きなものではない)
ただ、自分でプログラムを作れば、ある意味で何でも出来ることになります。
つまり市販されているもの(前述のリスト2に相当)の中にはソースコードが
添付されていないものもあり、新たにプログラムに付加したい機能があっても
プログラムに手を加えたり、改良を施すことが非常に困難な場合があります。
これに対してプログラムを自分で作れば、自分の思いのままの機能を自由に付
加、拡張することができます(何でも拡張できるという訳ではないし、作成し
た人物の力量にも強く依存します)。
(むしろ、貴重な才能、労力、時間が浪費されること
が問題)
無論、もともとのバンド屋さんがいままで自分の持っていたプログラムに愛
想を尽かして、心気一転新しいプログラムに作り直す(正直バンド屋にとって
これは大変勇気が必要です)、或いは従来(これまで)にない新手法、概念に
よるプログラムを新規開発することを何ら妨げるものではありません。
リスト5は、(自力での開発能力はなく、かつ有償、無償に関わらず人のも
のを使いたくないけれど)どうしても手許にプログラムが欲しいと言う人のた
めのものです。問題はどこに頼むかと、どのくらい費用がかかるかです。当然、
バンド計算プログラムを作ることが依頼できる機関は限られます。更に、多分、
バンド計算プログラム1本で、最低でも数百万円以上の費用が必要と思われま
す。
時間はないが、予算が沢山ある場合にはお勧めできるかもしれません。ただ
しこれは市販のパッケージを買うのと大して変わりません。ソースコードが確
実についていることと、技術上の支援が受けられること(これは契約の内容、
条件に依ります)、著作権は作成を依頼した側が保有することができる(よう
に契約する←つまり自分達のものに出来る)ことが有利な点と言えます。
リスト6は、計算そのものを外注によって代行してもらう手です。最近この
ような外注を受けるところがいくつか存在します。ただ、筆者自身外注の経験
がなく、詳細を語るほどの知識、情報がありません。このため、これに関して
はこれ以上の言及はしないこととします。
リスト7は、例えば最近注目される活動としてCMDワークショップなどに
参加してみることも良い選択の一つと思われます。このワークショップの開催
場所は主に国際高等研究所(京都)
です。
他にもこのような企画、催しがあるかもしれませんが、筆者は知りません
(単なるセミナー、報告会のようなものならありますが)。”バンド計算夏の学校”みたなものがあれば面白い
のですが、、、。
リスト8は、オンライン上にある掲示板に質問してみたり、バンド計算コー
ド関連のメイリングリストに参加して、そこで分からないことを尋ねてみる。
取り敢えずそれをとっかかりとして次にどのような選択肢を選ぶために役立て
ることは可能でしょう。
リスト9、、、最も妥当な判断かもしれません^^;。
次に対象となる研究者の分野で考えてみたいと思います。対象となるのが所
謂物理の理論出身で、量子力学を一通り学んで(成積不問)いたら上記リスト
の2、3、4のどれでも挑戦できると思います。群論や、FORTRAN等、
計算機に強ければ尚可。
物理出身の実験屋さんは、もし量子力学や群論や計算機(+FORTRAN
その他)に自身があれば2、3、4、5も可能(かもしれない)ですが、自分
としてはやはり1を勧めます。
量子力学や群論や計算機(+FORTRAN)のどれにも自信のない理論屋、
実験屋は、迷わず1を勧めます。4、5は間違った選択です、2、3はするな
とは言いませんが、結果は保証できませんし恥をかいても知りません。6、7
は今の日本のバンド計算の現状では場合によっては賢明な選択になるかもしれ
ません。
日本(多分海外でも)では、バンド計算請負業のような組織、機関、グルー
プはありません(←実は、存在するようなのですが詳細は筆者も知りません)。
上記リスト1のように、共同研究という形でバンド計算を依頼する場合どのよ
うにしたら良いのか、以下に示したいと思います。
まず自分の所属する組織、機関、部門、課などの中にバンド屋さんがいない
か探してみます。意外にバンド屋さんは身近にいるものです。もしいたら、そ
して顔見知りだったら、早速接触(コンタクト)を図ってみると良いと思いま
す。全く面識がなければ、同僚でそのバンド屋さんを知っている人を探し、紹
介してもらうと良いでしょう。いずれの場合でも相手がどのようなバンド計算
手法を使っているか、どのような系を今扱っているか、そして忙しそうか、暇
そうかなどを事前に調べておくと良いと思います。バンド計算は実は大変泥臭
い研究分野でありまして、大変な労力を注ぎ込んだ割には成果が乏しい場合が
よくあります。お目当てのバンド屋さんが大変忙しい場合もあり、バンド計算
してくれと頼んでもあっさり断られてしまう可能性もあります。その時は、こ
のバンド屋さんは大変忙しのだろうということで許してやってくださ
い。
計算を依頼する系や、望みの結果がバンド屋さんの使っている、または使え
る手法では計算できない場合もあります。多分その時はバンド屋さんからそれ
はここでは出来ないと言われると思います。その時は他の機関のバンド屋さん
には出来るかも知れないので、一応その旨聞いてみると良いでしょう。場合に
よっては計算可能なバンド屋さんを紹介してもらえる可能性があります。
ただ現行のバンド計算手法では土台計算が無理なものもあります。その場合
は依頼されたバンド屋さんが、それはどうやっても無理と指摘すると思います。
その時は素直に諦めましょう。当然、将来はできる可能性があると思
いますのであまり悲観しないでください。
近くにバンド屋さんが見当たらない場合、同僚の中で物理出身者(理論だと
尚可)がいれば、その”つて”でバンド屋さんまで辿れるかもしれません。も
し辿れれば紹介してもらうなり、FAX番号やe-mailアドレスが分っていれば、
FAXなりメイルで連絡をとれば良いと思います。【電話での連絡はやめた方
が良いと思います。】
参考ページ[日本バンド屋さんマップ
]
【重要】
いきなり、FAXやe-mailでバンド計算(或いは共同研究)の依頼をする場
合は常識的な礼節をわきまえて行なってください。
もし全くつてもコネも無い場合は、日本物理学会に参加して探すという手が
あります。おそらく国内でバンド屋さんが一番よく集まる大きな学会としては
日本物理学会が筆頭に挙げられます。日本物理学会は年に2回(年次大会〔年
会〕と春(または秋←普通は、秋)季大会、特に春(または秋)季大会は素粒
子系と物性系とが別々の会場で行なわれるので注意→当面オンライン実施)あ
り、筆者は2025年3月の日本物理学会春季大会(オンライン開催)での講
演予定はありません。次の応用物理学会春季学術講演会(2025年春季、
東京理科大野田キャンパス)での講演予定もありません。これらの学会に参加
(参加費はちゃんと受付で払って下さい〔←可能なら事前参加登録す
る〕)して講演プログラムを入手し(最近はオンラインでも閲覧可能な場合が
多い)、講演題目の中で、”第一原理”とか”バンド計算”とか”電子状態”
とか書かれているものを探し出し、その講演を聞いてみて依頼可能そうだった
ら、そのセッション終了後に接触を図ってみると良いかもしれません。
バンド屋さんが比較的、沢山いるセッション(この分野別の表記は、最近大
幅に変更されています。”領域”という呼び方になっています。詳細は日本物
理学会[ページ]をご参照下さい)等は、
オンライン上で学会講演プログラム内容を検索可能なので、バンド計算に関し
てのキーワード(”第一原理”、”バンド”、”電子構造”、”電子状態”、”
理論計算”等々)から検索を行なうのは非常に有効と思われます。
【関連重要情報】
[先頭][総目次
][最初に戻る][やさしい(?)バンド計算プログラムの作り方
]

